Calculus 3

• Calculus 3, Topic 1: The Plane (47:04) the real line and coordinates; the Euclidean plane, rectangular and polar coordinates; vectors and vector arithmetic (including scaling, addition, and magnitude); the standard basis.
• Calculus 3, Topic 2: Euclidean 3-space (48:30) points in rectangular, cylindrical, and spherical coordinates; vectors in 3 dimensions.<
• Calculus 3, Topic 3: The dot product (48:28) Parallel and orthogonal vectors; the Dot Product and its Law of Cosines; vector projections; and an explanation of the negative reciprocal rule for slopes.
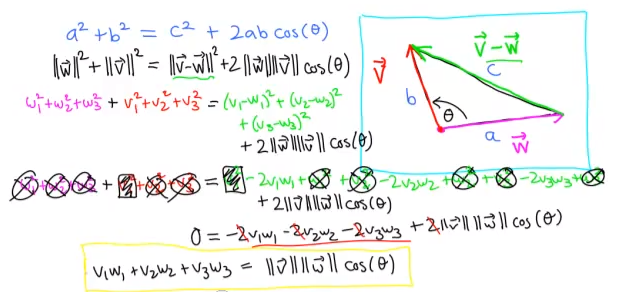
• Calculus 3, Topic 4: The cross product (48:25) Derivation of the cross product and its key geometric properties.
• Calculus 3, Topic 5: Planes and lines in space (48:14) The equation of a plane (normal and standard form); the equations of a line (symmetric and parametric forms); with derivations and lots of examples
• Calculus 3, Topic 6: Vector-valued functions (41:31) A description of vector-valued functions, emphasizing their visualization in 2 and 3 dimensions. Topics include eliminating parameters and coordinate projections.
• Calculus 3, Topic 7: Vector-valued calculus (47:07) Applying basic calculus concepts (like limits, derivatives, and integrals) to vector-valued functions.
• Calculus 3, Topic 8: The components of motion (48:48) A description of the components of motion, including velocity, acceleration, the unit tangent and normal vectors, the tangential and normal components of acceleration, displacement, and arclength.
• Calculus 3, Topic 9: Surfaces and functions of several variables (46:53) An investigating of surfaces, including how they're expressed and how to plot them. We investigate their connection to functions of 1 and 2 variables.
• Calculus 3, Topic 10: Limits in several variables (43:19) A look at domains and limits of functions of 2 and 3 variables; techniques for computing limits; and continuity in several variables.
• Calculus 3, Topic 11: Partial derivatives (50:31) Motivating partial derivatives; examining their computation and notation; higher-order derivatives and the equality of mixed partials.
• Calculus 3, Topic 12: Differentiability in two variables (48:59) We deduce the formula for a tangent plane and use it show why the existence of partial derivatives is not a good definition for differentiability. We then give a better one and look at some consequences.
• Calculus 3, Topic 13: The gradient (51:32) We introduce the gradient and directional derivatives, and argue that the gradient is the proper "derivative" object in several variables. We also discuss the important analytic and geometric properties of the gradient, and extend the results to 3 variables.
• Calculus 3, Topic 14: The multivariable Chain Rule (45:00) A look at the various Chain Rule variations for Calculus 3, including examples of its use. We also look at its application to implicit differentiation in 1 or more variables.
• Calculus 3, Topic 15: Local extrema in 2 variables (46:18) A description of local extrema and saddles, including finding them using the gradient and classifying them using the Second Derivative Test.
• Calculus 3, Topic 16: Constrained extrema (57:44) A description of global and constrained extrema, and techniques to determine them, including the method of Lagrange multipliers and the Extreme Value Theorem.
• Calculus 3, Topic 17: Double integrals over rectangles (47:03) We introduce the 2-variable integration concept: double integrals over a rectangle. We also discuss Fubini's Theorem and the relationship between double and iterated integrals.
• Calculus 3, Topic 18: Double integrals over regions (59:24) We define the double integral of a function of 2 variables over a general region in the plane, discuss Fubini's Theorem, and look at several examples.
• Calculus 3, Topic 19: Triple integrals (53:47) A description of triple integrals, their calculation with Fubini's Theorem, and their interpretation as mass and volume.
• Calculus 3, Topic 20: Integration in coordinate systems (56:02) We discuss the change of coordinate formulas for integrating with respect to polar, cylindrical, and spherical coordinates.
• Calculus 3, Topic 21: Line integrals (45:41) A discussion of scalar line integrals, including their evaluation using parametrized curves and their applications to linear mass and arclength.
• Calculus 3, Topic 22: Vector fields (50:03) A discussion of vector fields and the application of calculus ideas (visualization, continuity, derivatives, and integrals) to them.
• Calculus 3, Topic 23: Conservative vector fields (52:38) A discussion of conservative, path independent, and gradient vector fields, and the relationships between these concepts.
• Calculus 3, Topic 24: Green's Theorem (46:46) A discussion of Green's Theorem, and its connection with the different integral (and derivative and vector!) concepts discussed so far.